El universo de von Neumann lo podemos ver a través de niveles medidos por números ordinales, como $V_{\alpha}$ y explícitamente ahí entra en juego la noción de rango, la cual nos indica qué tan complicado es un conjunto $x$ dentro del universo. Por ejemplo, es natural pensar que el conjunto $2=\left\lbrace{\emptyset , 1}\right\rbrace$ es más complejo que $1=\left\lbrace{\emptyset}\right\rbrace$ y bajo esta idea nace la función rango.
Sea $A$ una clase y $R$ una relación bien fundada en $A$ y $b\in A$, definimos el rango como:
\begin{align*} ran(b)= \bigcup\left\lbrace{S(ran(x)):x \in pred_{A,R}(b)}\right\rbrace \end{align*}
Sin embargo, como su definición es recursiva es necesario usar el Teorema de Recursión. \begin{align*} G(a,b)= \bigcup\left\lbrace{S(t):t\in Im(b)}\right\rbrace\\\\ F(a) = G(a,F\restriction_{pred_{A,R}(a)}) =\\\\ \bigcup\left\lbrace{S(F(c)):c\in pred_{A,R}(a)}\right\rbrace \end{align*}
Al ser definido bajo una recursión transfinita, podemos decir las siguientes propiedades
1) $ran(x)$ es un número ordinal
2) Si $x$ es un predecesor de $y$ entonces $S(ran(x))\leq ran(y)\implies ran(x)< ran(y)$
Finalmente, para ayudarnos a entender la función rango y sus propiedades es apropiado dibujarlo
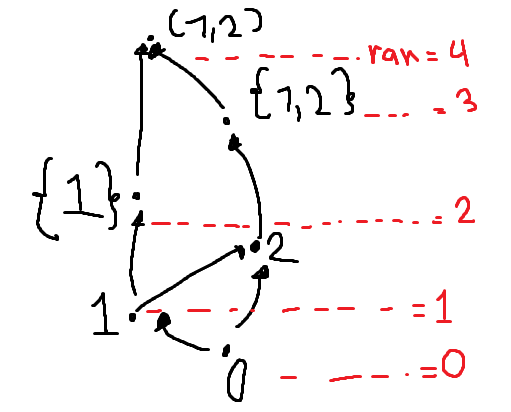Basado en el vídeo de Jesus Nieto Martinez sobre Teoria de Conjuntos